Pascal's triangle is a useful recursive definition that tells us the coefficients in the expansion of the polynomial (x + a)^n. Each...
X287: Recursion Programming Exercise: Pascal Triangle
Pascal's triangle is a useful recursive definition that tells us the coefficients in the expansion of the polynomial (x + a)^n. Each element in the triangle has a coordinate, given by the row it is on and its position in the row (which you could call a column). Every number in Pascals triangle is defined as the sum of the item above it and the item above it and to the left. If there is a position that does not have an entry, we treat it as if we had a 0 there.
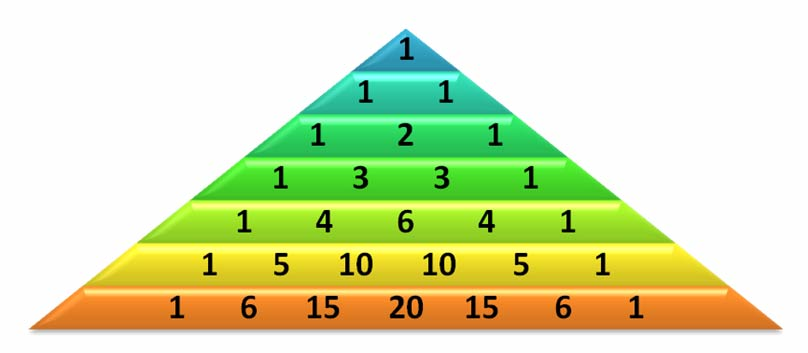
Given the following recursive function signature, write the recursive function that takes a row and a column and finds the value at that position in the triangle. Assume that the triangle starts at row 0 and column 0.
Examples:
pascal(2, 1) -> 2
pascal(1, 2) -> 0
Your Answer:
Feedback
Your feedback will appear here when you check your answer.
